|
|
|
|
|
Глава X. Метод координат Задачи повышенной трудности к главе X. Метод координат1256. Вершины четырёхугольника ABCD имеют координаты А (х1; у1), В (х2; у2), С (х3; у3) и D(x4; y4). Докажите, что этот четырёхугольник является параллелограммом тогда и только тогда, когда х1 + х3 = х2 + х4 и у1 + у3 = у2 + у4. 1257. Даны две точки А (х1; у1) и В (х2; у2). Докажите, что координаты (х; у) точки С, делящей отрезок АВ в отношении λ 1258. Из физики известно, что центр тяжести однородной треугольной пластинки находится в точке пересечения медиан. Найдите координаты центра тяжести такой пластинки, если координаты её вершин равны: (х1; у1), (х2; у2), (х3; у3). 1259. Вершины треугольника АВС имеют координаты А (-3; 0), В (0; 4), С (3; 0). Биссектриса угла А пересекает сторону ВС в точке D. Найдите координаты точки D. 1260. В треугольнике АВС АС = 9 см, ВС= 12 см. Медианы AM и BN взаимно перпендикулярны. Найдите АВ. 1261. Найдите координаты центра тяжести системы трёх масс m1, m2 и m3, сосредоточенных соответственно в точках А1 (х1; у1), А12 (х2; у2), А3 (х3; у3). 1262. В каждом из следующих случаев на оси абсцисс найдите точку М, для которой сумма её расстояний от точек А и В имеет наименьшее значение: а) А (2; 3), В (4;-5);
1263. Докажите, что: а) уравнение Ах + By + С = 0, где А и В одновременно не равны нулю, является уравнением прямой;
1264. Найдите точки пересечения двух окружностей, заданных уравнениями (x - 1)2 + (у - 2)2 = 4 и х2 + у2 = 1, и вычислите длину их общей хорды. 1265. Даны три точки А, В, С и три числа α, β, γ. Найдите множество всех точек М, для каждой из которых сумма αАМ2 + βВМ2 + γСМ2 имеет постоянное значение, если: а) α + β + γ ≠ 0;
1266. Даны прямая а и точка А, не лежащая на ней. Для каждой точки Мх прямой а на луче АМ1 взята такая точка М, что АМХ • AM = k, где k — данное положительное число. Найдите множество всех точек М. 1267. Точка О не лежит на данной окружности. Для каждой точки Мj окружности на луче OM1 взята такая точка М, что ОМ = k • OM1, где k — данное положительное число. Найдите множество всех точек М. 1268. Пусть А и В — данные точки, k — данное положительное число, не равное 1. а) Докажите, что множество всех точек М, удовлетворяющих условию AM = kBM, есть окружность (окружность Аполлония).
|
|
|



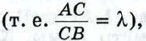 выражаются формулами
выражаются формулами